Note 5: Tree
Concept in Data Structure for Application
The Concept of The Tree
It implies that we organize the data so that items of information are related by the branches.
Definition: A tree is a finite set of one or more nodes such that:
- There is a specially designated node called the root.
- The remaining nodes are partitioned into n ³ 0 disjoint sets T1,…, Tn, where each of these sets is a tree. We call T1,…, Tn the subtrees of the root.
Terminology
Root of the tree: The top node of the tree that is not a subtree to other node, and has two children of subtrees.
Node: It is stands for the item of information and the branches to other nodes.
The degree of a node: It is the number of subtrees of the node.
The degree of a tree: It is the maximum degree of the nodes in the tree
The parent node: a node that has subtrees is the parent of the roots of the subtrees
The child node: a node that is the roots of the subtrees are the children of the node
The Level of the tree: We define the level of a node by initially letting the root be at
level one
The depth of a tree: It also called height of a tree. It is the maximum level of any node
in the tree
Type of The Tree
General Tree
Full Tree
Complete Tree
Binary Tree
Binary Search Tree
The Heap
The representation of node in the tree structure:
|
data |
|
|
left child |
right child |
Define Structure Node for the tree:
typedef struct node *ptr_node;
sturct node
{
short data;
ptr_node left_child;
ptr_node right_child;
}
General Tree Graphical Picture:
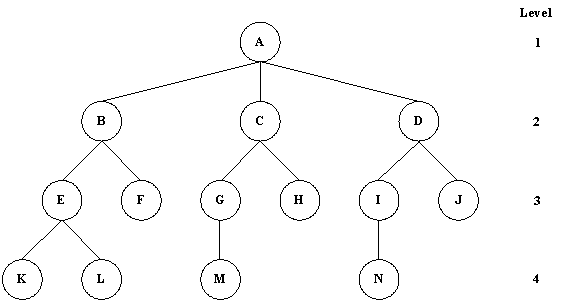
Binary Tree
Definition: A binary tree is a finite set of nodes that is either empty or consists of a root
and two disjoint binary trees called the left subtree and the right subtree.
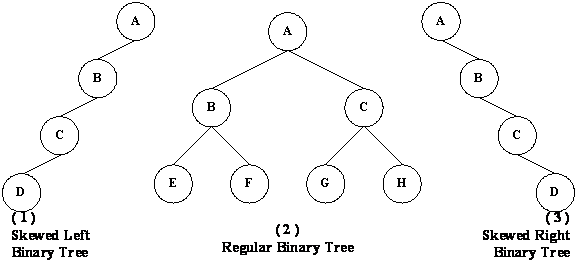
Binary Tree Types:
Regular Binary Tree ( 2 )
Skewed Left Binary Tree ( 1 )
Skewed Right Binary Tree ( 3 )
Three Graphical Pictures of the Binary Tree:
Properties of Binary Trees
In particular, we want to find out the maximum number of nodes in a binary tree of depth k, and the number of leaf nodes and the number of nodes of degree two in a binary tree. We present both these observations as lemma.
Lemma 5.1 [Maximum number of nodes]:
(1) The maximum number of nodes on level i of a binary tree is 2i-1, i ³ 1
(2) The maximum number of nodes in a binary tree of depth k is 2k – 1, k ³ 1
Lemma 5.2 [Relation between number of leaf nodes and
nodes of degree 2]:
Nonempty binary tree, T, if n0 is the number of leaf nodes and n2 the number of nodes of degree 2, then n0 = n2 + 1.
Binary Tree Representations
Array Representation
The numbering scheme used in it suggests out first representation of a binary tree in memory. Since the nodes are numbered from 1 to n, we can use a one-dimensional array to store the nodes. (We do not use the 0th position of the array.) Using Lemma 5.1 we can easily determine the locations of the parent, left child, and right child of any node, i, in the binary tree.
Lemma 5.3:
If a complete binary tree with n nodes (depth = ë log2n +1 û ) is represented sequentially, then for any node with index i, 1 £ i £ n, we have:
(1) parent ( i ) is at ë i / 2 û if i ¹ 1 if i = 1, i is at the root and has no parent
(2) left_child( i ) is at 2i if 2i £ n. If 2i > n, then i has no left child
(3) rightt_child( i ) is at 2i + 1 if 2i + 1 £ n. If 2i + 1 > n, then i has no right child
Linked Representation
While the sequential representation is acceptable for complete binary trees, it wastes space for many other binary trees. In, addition, this representation suffers from the general inadequacies of other sequential representations. Thus, insertion or deletion of nodes from the middle of a tree requires the movement of potentially many nodes to reflect the change in the level of these nodes. We can easily overcome these problems by using a linked representation. Each node has three fields, left_child, data, and right_child as two pictures show the node representation of the binary tree below:

Binary Tree Traversals
There are many operations that we can perform on tree, but one that arises frequently is traversing a tree, that is, visiting each node in the tree exactly once. A full traversal produces a linear order for the information in a tree.
Binary Tree Traversals Types
Inorder Traversal (Left, Parent, Right)
Preorder Traversal (Parent, Left, Right)
Postorder Traversal (Left, Right, Parent)
Level Order Traversal (Top to Bottom, Left to Right)
Example of the Binary Tree:
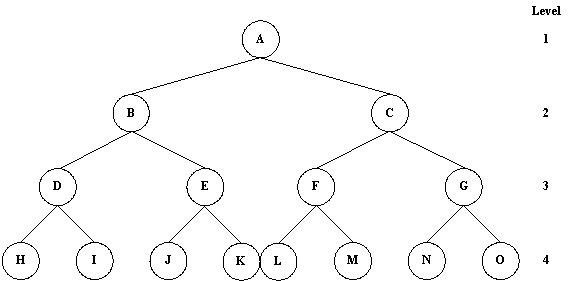
Binary Tree Traversals Functions
Inorder Tree Traversal
Recursive function:
void inorder (ptr_node ptr)
{
if (ptr)
{
inorder (ptr->left_child);
cout << ptr->data;
inorder (ptr->right_child);
}
}
Result of binary tree example:
H, D, I, B, J, E, K, A, L, F, M, C, N, G, O
Preorder Tree Traversal
Recursive function:
void preorder (ptr_node ptr)
{
if (ptr)
{
cout << ptr->data;
preorder (ptr->left_child);
preorder (ptr->right_child);
}
}
Result of binary tree example:
A, B, D, H, I, E, J, K, C, F, L, M, G, N, O
Postorder Tree Traversal
Recursive function:
void postorder (ptr_node ptr)
{
if (ptr)
{
postorder (ptr->left_child);
postorder (ptr->right_child);
cout << ptr->data;
}
}
Result of binary tree example:
H, I, D, J, K, E, B, L, M, F, N, O, G, C, A
Level Order Tree Traversal
Using queue:
void level_order (ptr_node ptr)
{
int front = rear = 0;
ptr_node queue[max_queue_size];
if (!ptr) // empty tree;
return;
addq(front, &rear, ptr);
for ( ; ; )
{
ptr = deleteq (&front, rear);
if (ptr)
{
cout << ptr->data;
if (ptr->left_child)
addq (front, &rear, ptr->left_child);
if (ptr->right_child)
addq (front, &rear, ptr->right_child);
}
else
Break;
}
}
Result of binary tree example:
A, B, C, D, E, F, G, H, I, J, K, L, M, N, O
Binary Search Tree
Definition: A binary search tree is a binary tree. It may be empty. If it is not empty, it satisfies the following properties:
(1) Every element has a key, and no two elements have the same key, that is, the keys are unique.
(2) The keys in a nonempty left subtree must be smaller than the key in the root of the subtree.
(3) The keys in a nonempty right subtree must be larger than the key in the root of the subtree.
(4) The left and right subtrees are also binary search trees.
Example of the Binary Search Tree:
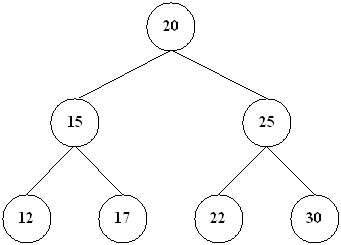
Searching A Binary Search Tree
Suppose we wish to search for an element with a key. We begin at the root. If the root is NULL, the search tree contains no elements and the search is unsuccessful. Otherwise, we compare key with the key value in root. If key equals root’s key value, then the search terminates successfully. If key is less than root’s key value, then no elements in the right subtree subtree can have a key value equal to key. Therefore, we search the left subtree of root. If key is larger than root’s key value, we search the right subtree of root.
Recursive Function for Binary Search Tree:
tree_ptr search ( tree_ptr root, int key )
{
if ( !=root )
return NULL;
if ( key = = root->data )
return root;
if ( key < root->data )
return search ( root->left_child, key );
return search ( root->right_child, key );
}
Inserting Into A Binary Search Tree
To insert a new element, key, we must first verify that the key is different from those of existing elements. To do this we search the tree. If the search is unsuccessful, then we insert the element at the point the search terminated.
Insert Function:
void insert_node (
tree_ptr *node, int num )
{
tree_ptr ptr, temp = modified_search ( *node, num ); // **
if ( temp || ! ( *node ) )
{
ptr = new node;
if ( ptr = = NULL)
{
cout << “The memory is full \n”;
exit ( 1 );
}
ptr->data = num;
ptr->left_child = ptr->right_child = NULL;
if ( *node )
{
if ( num < temp->data )
temp->left_child = ptr;
else
temp->right_child = ptr;
}
else
*node = ptr;
}
}
** The function modified_search that is slightly modified version of function search. This function searches the binary search tree *node for the key num. If the tree is empty or if num is present, it returns NULL. Otherwise, it returns a pointer to the last node of the tree that was encountered during the search. The new element is to be inserted as a child of this node.
Deletion from a Binary Search Tree
- Deletion of a leaf node is easy. For example, if a leaf node is left child, we set the left child field of its parent to NULL and free the node.
- The deletion of a nonleaf node that has only a single child is also easy. We erase the node and then place the single child in the place of the erased node.
- When we delete a nonleaf node with two children, we replace the node with either the largest element in its left subtree or the smallest elements in its right subtree. Then we proceed by deleting this replacing element from the subtree from which it was taken.
The Heap
Two type of the heap: Max Heaps and Min Heaps.
Definition
Max Heaps: A max tree is a tree in which the key value in each node is no smaller than the key values in its children (if any). A max heap is a complete binary tree that is also a max tree.
Min Heaps: A min tree is a tree in which the key value in each node is no larger than the key values in its children (if any). A min heap is a complete binary tree that is also a min tree.
Following insert and delete operation for max heap are using array representation:
Define Max Heap Structure
#define MAX_ELEMENTS 200 /* maximum heap size+1 */
#define HEAP_FULL (n) ( n = = MAX_ELEMENTS-1 )
#define HEAP_EMPTY (n) ( !n )
struct element
{
int key;
/* other fields */
}
element heap [MAX_ELEMENTS];
int n = 0;
Insertion Into A Max Heap
void insert_max_heap ( element item, int *n )
{
int i;
if ( HEAP_FULL ( *n ) )
{
cout << “The heap is full! \n”;
exit ( 1 );
}
i = + + ( *n );
while ( ( i != 1 ) && ( item.key > heap[ i / 2 ].key ) )
{
heap[ i ] = heap[ i / 2 ];
i / = 2;
}
heap[ i ] = item;
}
Deletion From A Max Heap
element delete_max_heap ( int *n )
{
int parent, child;
element item, temp;
if ( HEAP_EMPTY ( *n ) )
{
cout << “The heap is empty! \n”;
exit ( 1 );
}
//save value of the element with the highest key
item = heap[1];
//use last element in heap to adjust heap
temp = heap[ ( *n ) - - ];
parent = 1;
child = 2;
while ( child < = *n )
{
//find the larger child of the current parent
if ( child < *n ) && ( heap[ child ].key < heap[ child + 1 ].key)
child + +;
if ( temp.key >= heap[ child ].key )
break;
//move to the next lower level
heap[ parent ] = heap[ child ];
parent = child;
child * = 2;
}
heap[ parent ] = temp’
return item;
}